LC吐血整理之Dynamic Programming篇

Posted on | In
人生苦短 我学python

所有题解方法请移步 github-Leecode_summary

70.爬楼梯

讲一下最容易理解的两个方法（以n = 6为例）： 1.暴力穷举法： 每一步都有两种走法，直接穷举处所有走法，不符合要求的删除

  • 符合要求的分支+1:

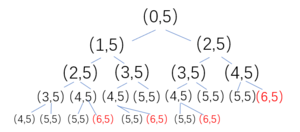
  • 关键函数:

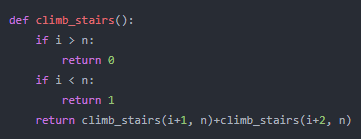
2. 动态规划法: 到达第 ii 阶的方法总数就是到第 (i-1)(i−1) 阶和第 (i-2)(i−2) 阶的方法数之和
关键函数：ct[i] = ct[i-1] + ct[i-2]　(climb_stairs[i] 表示到达i阶的方法数)
　　　　　上述ct[i]实际上也是第i个斐波那契数

62&63. 不同路径 I&II

不同路径 I: 是一个很经典排列组合题目，不过动态规划方法和70题类似，把一维换成了二维来思考，emmm说不定明天就变成三维了。
不同路径 II: 这个题目想通了也不算难，重点在第一行第一列的一个初始化和obstacleGrid[i][j] == 1时的处理，话不多说看具体代码吧。

120.三角形最小路径和

动态规划不愧为动态规划，看的我是一愣一愣的，真的挺有趣的 两种解决思路: 1.带记忆的自顶向下 2.取最小值的自底向上

279.完全平方和

说实话我的做法也是来源于120的思路，先 math.floor(math.sqrt(n))得到构建的基础数组li ，然后遍历相加（每一层中每一个数遍历相加li），该层出现目标数组，则break并返回层数，画个图看看： 应该容易看懂的图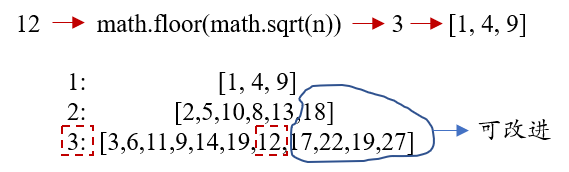： 应该容易看懂 另外，用动态规划法，要求n个数的最小平方和，感觉会超时…

又是久违的Tips-1: 今日份的Tips: python中如何跳出多重循环
我傻逼了，直接用return就好了，我还查了半天怎么跳出多重循环，晕… 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 方法一：直接return，也可以包装成函数return
# 方法二：最傻的 立flag
# 方法二：for...else... 怎么样第一次见吧,我也是第一次见
while 1:
    for i in range(10):
        for j in range(6):
            if j == 4:
                break
        else:
            continue
        break
    else:
        continue
    break
return "out"
# 方法三：try...except...
class res(Exception):
    pass
try:
    while 1:
        for i in range(10):
            for j in range(6):
                if j == 4:
                    raise out
except out:
    return "out"

Tips-2:
原来还有一个叫四平方定理的东西？？ 四平方定理：任何一个正整数都可以表示成不超过四个整数的平方之和。
推论：满足四数平方和定理的数n（四个整数的情况），必定满足 n=4^a(8b+7)