知识来源:
机器学习 ,也就是传说中的西瓜书,by周志华
统计学习方法,真的是满满的干货,知识丰富,by李航
网上各种干货精选
转自的一张思维导图:
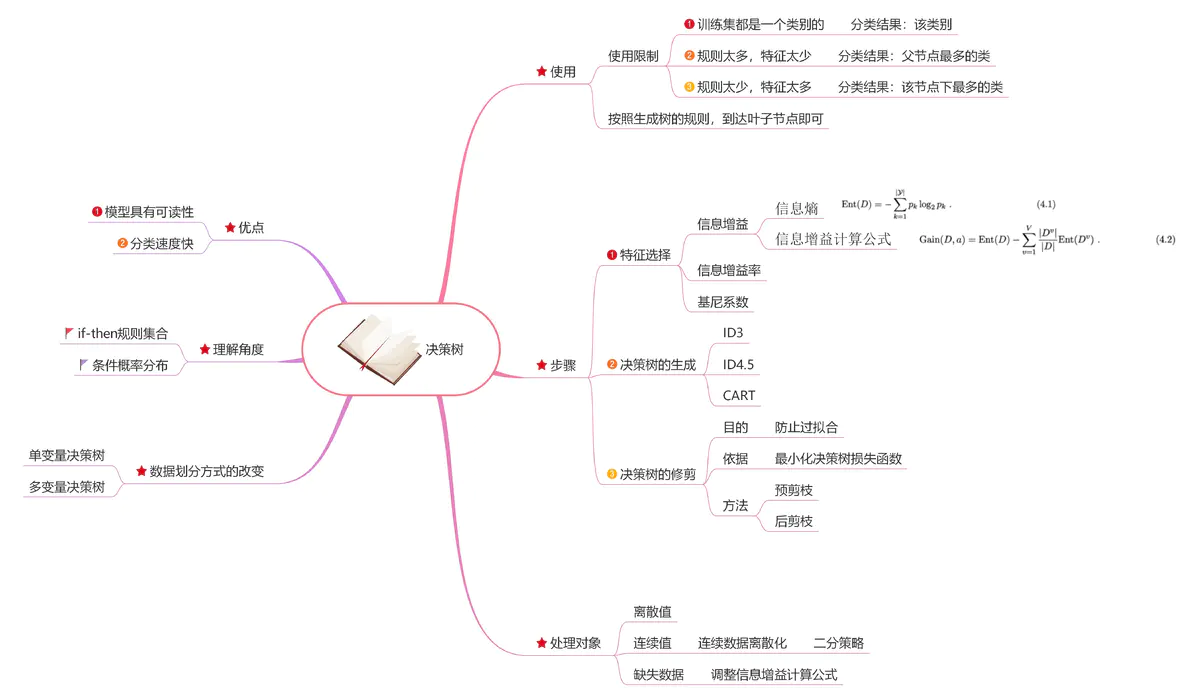
定义
决策数基于树结构进行决策的一种基本的分类与回归方法,定义在特征空间与类空间上的条件概率分布,决策树学习的损失函数通常为正则化的极大似然估计,学习策略是以损失函数为目标函数的最小化。
决策树的学习包含三个步骤:特征选择、模型生成、剪枝。
一般决策树包含一个根结点、若干内部结点和若干个叶结点,叶结点对应决策结果,其他每个结点则对应于一个属性测试,目的是为了产生一棵泛化能力强即处理未见示例能力强的决策树,“分而治之”
决策树的生成是一个递归过程(三种情形导致递归返回):①当前节点包含样本属于同一类别,无需划分 ②当前属性集为空或是样本在所有属性上取值相同,无需划分 ③当前结点包含的样本集合为空,不能划分
②③情况下将当前结点标记为叶结点 ②利用的是当前结点的后验分布③是将父结点的样本分布作为当前结点的先验分布
基本流程
生成结点,输入训练集和属性集,是否递归结束,否则选择最优划分属性继续划分
划分选择
也就是如何选择最优的划分属性
信息增益
在信息论与概率论中,熵用于表示随机变量不确定性的度量。
信息增益利用了“信息熵”的概念:Gain(D, a)=经验熵H(D)-经验条件熵H(D|a),具体求解公式如下:
$$\operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|}p_{k}\log_{2}p_{k}$$
$$\operatorname{Gain}(D, a)=\operatorname{Ent}(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right)$$
信息增益越大,则意味着使用属性a来进行划分所获得的”纯度提升”越大(y表示类别,v表示属性取值,a为某个具体属性)
信息增益表示的是:得知特征a的信息而使得类y的信息的不确定性减少的程度
ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征
优点: 理论清晰、方法简单、学习能力较强
缺点: ①只能处理分类属性的数据,不能处理连续的数据;②划分过程会由于子集规模过小而造成统计特征不充分而停止;③ID3算法在选择根节点和各内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息。
增益率
增益比Gain_ratio(D, a)= Gain(D, a)/训练数据集关于特征a的值的熵 $$\text { Gain ratio }(D, a)=\frac{\operatorname{Gain}(D, a)}{IV(a)}$$ 其中: $$\mathrm{IV}(a)=-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \log _{2} \frac{\left|D^{v}\right|}{|D|}$$ 信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,可以采用增益率进行划分属性选择 增益率准则对可取值数目较少的属性有所偏好,C4.5算法的核心是在决策树各个结点上应用增益率选择特征,但C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式: 先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
基尼指数
$$\begin{aligned}\operatorname{Gini}(D) &=\sum_{k=1}^{|\mathcal{Y}|} \sum_{k^{\prime} \neq k} p_{k} p_{k^{\prime}}=1-\sum_{k=1}^{|\mathcal{Y}|} p_{k}^{2}\end{aligned}$$
直观来说,Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此,Gini(D)越小,则数据集D的纯度越高。
$$\text {Gini_index}(D, a)=\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Gini}\left(D^{v}\right)$$
CART算法的核心是在决策树各个结点上应用增益率选择特征,CART生成的树只能是二叉树,而前两者可生成多叉树。
Gini指数和熵都可以表示数据分布的不确定性,那有啥区别呢? ①Gini指数不需要对数运算,更加高效 ②Gini指数数据更偏向于连续属性,熵更偏向于离散属性
剪枝
剪枝 (pruning)是决策树学习算法对付“过拟合”的主要手段,基本策略有“预剪枝”(prepruning)和“后剪枝”(postpruning)
预剪枝与后剪枝的优缺点??(欠拟合程度、时间复杂度)
连续值处理
处理连续值需要确定划分点,可将划分点设为该属性在训练集中出现的不大于中位点的最大值,从而使得最终决策树使用的划分点都在训练集中出现过
注意:与离散属性不同,若当前结点划分属性为连续属性,该属性还可作为其后代结点的划分属性。
C4.5采用二分法对连续属性进行处理,先将特征取值排序,以连续两个值中间值作为划分标准,尝试每一种划分,并计算修正后的信息增益,选择信息增益最大的分裂点作为该属性的分裂点。
缺失值处理
举个栗子:C4.5生成过程
可重新定义信息增益计算式:
$$\begin{aligned}\operatorname{Gain}(D, a) &=\rho \times \operatorname{Gain}(\tilde{D}, a)=\rho \times\left(\operatorname{Ent}(\tilde{D})-\sum_{v=1}^{V} \tilde{r}_{v} \operatorname{Ent}\left(\tilde{D}^{v}\right)\right)\end{aligned}$$
其中ρ表示无缺失样本所占的比例,若样本x在划分属性a上取值未知,可对样本权值进行赋值,并以不同的概率划入不同的子结点中去,具体还是看书吧,一言两语说不明白。
多变量决策树
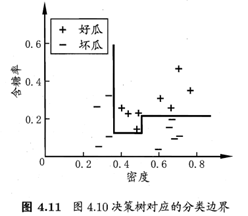
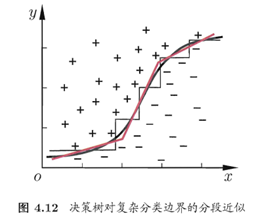
多变量决策树就是能实现”斜划分”甚至更复杂划分的决策树。
以实现斜划分的多变量决策树为例,在此类决策树中,非叶结点不再是仅对某个属性,而是对属性的线性组合进行测试。
每个非叶结点是一个形如$\sum_{i=1}^{d}w_{i}a_{i}=t$的线性分类器,其中$w_{i}$是属性$a_{i}$的权重,$w_{i}$和$t$可在该结点所含的样本集和属性集上学得。
优点
① 计算量小,模型可解释性强;
② 可处理有缺失属性值的样本;
③ 有非线性表达能力;
④ 决策树有些能直接处理类别特征,有些就不能。
总结一下
除信息增益、增益率、基尼指数之外,人们还设计了许多其他的准则用于决策树划分选择,有实验研究表明,这些准则虽然对决策树的尺寸有较大影响,但对泛化性能的影响很有限。 剪枝方法和程度对决策树泛化性能的影响相当显著,有实验研究表明,在数据带有噪声时通过剪枝甚至可将决策树的泛化性能提高25%。