知识来源：
机器学习 ，也就是传说中的西瓜书，by周志华
统计学习方法，真的是满满的干货，知识丰富，by李航
网上各种干货精选
基本形式
给定d个属性描述的示例$\boldsymbol{x}=\left(x_{1};x_{2};\ldots;x_{d}\right)$，其中$x_{i}$是$\boldsymbol{x}$在第i个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即： $$f(x)=w_{1} x_{1}+w_{2} x_{2}+\ldots+w_{d} x_{d}+b$$ 写成向量形式： $$f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$$
线性回归模型
线性回归
给定数据集$D={\left(\boldsymbol{x_{1}}, y_{1}\right),\left(\boldsymbol{x_{2}}, y_{2}\right), \dots,\left(\boldsymbol{x_{m}}, y_{m}\right)}$，其中$\boldsymbol{x_{i}}=\left(x_{i1};x_{i2};\ldots;x_{id}\right)$,$y_{i}\in\mathbb{R}$。
线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记，基本模型：
$$f\left(\boldsymbol{x_{i}}\right)=\boldsymbol{w^T}\boldsymbol{x_{i}}+b,使得 f\left(\boldsymbol{x_{i}}\right) \simeq y_{i}$$
基于均方误差最小化来进行模型求解的方法称为”最小二乘法”，在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。
上述样本$\boldsymbol{x}$由多个属性描述的线性回归称为多元线性回归，但在现实任务中，变量数可能大于样例数，或者d个属性不是线性无关的（多重共线性问题）,
可解出多个$\boldsymbol{w}$，都能使均方误差最小化，选择哪一个解作为输出，将由学习算法的归纳偏好决定，常见的做法是引入正则化项、PCA分析。
对数线性回归
假设我们认为示例所对应的输出标记是在指数尺度上变化，那就可将输出标记的对数作为线性模型逼近的目标，即:
$$\ln y=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$$
形式上是线性回归，但实质上已是在求取输入空间到输出空间的非线性函数映射。
更一般的，考虑单调可微函数$g(\cdot)$，令
$$y=g^{-1}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right)$$
这样得到的模型称为”广义线性模型”,其中函数$g(\cdot)$称为”联系函数”,对数线性回归是广义线性模型在$g(\cdot)=\ln (\cdot)$时的特例。
对数几率回归
对数几率回归（大名鼎鼎的逻辑回归logistic regression），是一种线性二分类模型，属于判别式模型。
逻辑回归初衷是将线性回归用于分类任务，可以理解为找到一个单调可微函数将分类任务的真实标记 y={0,1} 与线性回归模型的预测值 $z=\boldsymbol{w^{T}}\boldsymbol{x}+b$ 联系起来。
公式推导
对数几率函数$y=1/\left(1+e^{-z}\right)$（是Sigmoid函数最重要的代表）,令 $g(\cdot)=y$ 时得到： $$y=\frac{1}{1+e^{-\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right)}}$$ 进而可变换成： $$\ln \frac{y}{1-y}=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$$ 其中，$\frac{y}{1-y}$ 为“几率”，$\ln \frac{y}{1-y}$ 为对数几率。损失函数 (可以是ln也可以是log)
设$P\left(y=1|x\right)=f_{w,b}(x)$，$P\left(y=0|x\right)=1-f_{w,b}(x)$，逻辑回归采用极大似然估计来求模型参数w和b，对数似然函数为：
$$-ln\left(w, b\right)=\sum_{i=1}^{m}-y_{i} \ln \left(f_{w,b}(x_{i})\right)-\left(1-y_{i}\right) \ln \left(1-f_{w,b}(x_{i})\right)$$ 可以看到，逻辑回归损失函数为log损失(极大似然损失)，常用梯度下降法、牛顿法、拟牛顿法、共轭梯度下降法来解决。梯度下降参数迭代公式
$$w^{j}=w^{j}+\alpha \sum_{i=1}^{m} \left(y_{i}-f_{w,b}(x_{i})\right) x_{i}^{j}$$logistics模型
① 二分类模型 $$P(Y=1 | x)=\frac{\exp (\boldsymbol{w}^{\mathrm{T}} \cdot x+b)}{1+\exp (\boldsymbol{w}^{\mathrm{T}} \cdot x+b)}$$ $$P(Y=0 | x)=\frac{1}{1+\exp (\boldsymbol{w}^{\mathrm{T}} \cdot x+b)}$$ ② 多分类模型
逻辑回归的二分类问题可以扩展为多项逻辑回归模型： $$P(Y=i | x)=\frac{\exp \left(\boldsymbol{w_i}^{\mathrm{T}} \cdot x+b\right)}{1+\sum_{i=1}^{n-1} \exp \left(\boldsymbol{w_i}^{\mathrm{T}} \cdot x+b\right)}, i=1,2,3 \ldots, n-1$$ $$P(Y=n | x)=\frac{1}{1+\sum_{i=1}^{n-1} \exp \left(\boldsymbol{w_i}^{\mathrm{T}} \cdot x+b\right)}$$LR模型优缺点
优点：
① 直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确所带来的问题;
② 模型可解释性强，不仅预测出”类别”，还可得到近似概率预测，对许多需利用概率辅助决策的任务很有用;
③ 对数几率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解；
④ 模型简单，训练速度快； ⑤ 可根据系数w的大小判断特征重要性。缺点：
① 容易欠拟合，LR是一个线性模型，表达非线性能力比较弱；
② 一般的逻辑回归只能处理二分类任务，如果类别严格互斥可以用softmax多分类（否则就k个LR）；
③ 类别特征需要one-hot；
④ 如果特征之间线性相关，可能特征重要性将无法解释；
具体的线性回归和逻辑回归区别可参考coursea上吴恩达机器学习视频，讲的很详细。
最大熵模型
最大熵原理是概率模型学习的一个准则，最大熵原理认为，学习概率模型时，在所有可能的概率模型分布中，熵最大的模型是最好的模型。
这一部分有点没搞懂，Logistic回归与最大熵模型理论推导
逻辑回归Vs最大熵模型：
逻辑回归是最大熵对应为二类时的特殊情况，也就是说，当逻辑回归扩展为多类别的时候，就是最大熵模型。
线性判别分析
线性判别分析(Linear Discriminant Analysis)是一种经典的线性学习方法。
LDA的思想非常朴素: 给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。在对新样本进行分类时,
将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别，二维示意图如下：
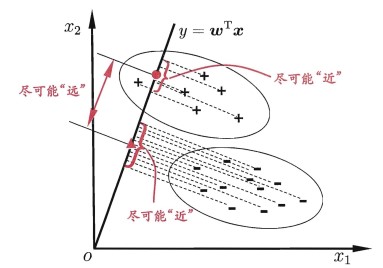
多分类学习
多分类方法一般采取一些基本策略利用二分类学习器来解决多分类问题，经典的拆分策略有OvO、OvR、MoM。
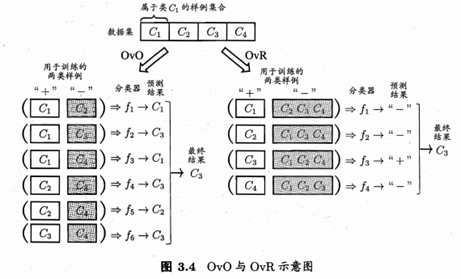OvR需要训练N个分类器，而OvO需训练N(N-1)/2个分类器， 因此，OvO的存储开销和测试时间开销通常比OvR更大，但在训练时，OvR的每个分类器均使用全部训练样例,
而OvO的每个分类器仅用到两个类的样例，因此，在类别很多时。OvO的训练时间开销通常比OvR更小,至于预测性能,则取决于具体的数据分布,在多数情形下两者差不多。
MvM 是每次将若干个类作为正类，若干个其他类作为反类.显然，OvO和OvR是MvM的特例，MvM的正、反类构造必须有特殊的设计，不能随意选取，常用策略有：”纠错输出码”(ECOC)。
类别不平衡问题
类别不平衡就是指分类任务中不同类别的训练样例数目差别很大的情况，基本策略有“再缩放”、“欠采样”、“过采样”、“阈值移动”。
- “再缩放”
以逻辑回归为例，正常情况下分类器决策规则为： $$若\frac{y}{1-y}>1则预测为正例$$ 当类别不平衡时，采用观测几率代替样本真实分布，修改决策规则为“只要分类器的预测几率高于观测几率就应判定为正例”： $$若\frac{y}{1-y}>\frac{m^{+}}{m^{-}}则预测为正例$$ 其中$m^{+}$为正例数，基于上式，将对率修改为： $$\frac{y^{\prime}}{1-y^{\prime}}=\frac{y}{1-y} \times \frac{m^{-}}{m^{+}}$$ 再缩放的思想虽简单，但实际操作却并不平凡，主要因为”训练集是真实样本总体的无偏采样”这个假设往往并不成立。 - “欠采样”
去除一些反例使得正、反例数日接近，然后再进行学习。（假设正例远少于反例）
欠采样法若随机丢弃反例可能丢失一些重要信息，欠采样法的代表性算法EasyEnsemble（利用集成学习机制，将反例划分为若干个集合供不同学习器使用，这样对每个学习器来看都进行了欠采样, 但在全局来看却不会丢失重要信息）。 - “过采样”
增加一些正例使得正、反例数目接近，然后再进行学习。
过采样法不能简单地对初始正例样本进行重复来样，否则会导致严重的过拟合，过采样法的代表性算法SMOTE（通过对训练集里的正例进行插值来产生额外的正例）。 - “阔值移动”
直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，将再缩放公式嵌入到其决策过程中。